Описание методики обучения учащихся темы «Параллельность прямых и плоскостей в курсе геометрии 7 – 11 классах»

Вывод: таким образом было рассмотрено примерное тематическое планирование темы, направленное на усвоение и отработку свойств параллельности прямых и плоскости.

Методика обучения базовому теоретическому материалу темы

1. Урок: « Параллельность прямые в пространстве». Консольные led светильники - консольные светильники уличного освещения agiro.ru.

Объяснение нового материала.

У: Каково может быть взаимное расположение двух прямых на плоскости (совпадают, пересекаются, являются параллельными)?

У: Дайте определение параллельных прямых на плоскости.

у: (

либо a не пересекает b).

У: Определение прямых в пространстве – то же.

У: Дан куб. Все грани – квадраты. Являются ли параллельные прямые АА1 и DD1, АА1 и СС1? Ответ обоснуйте. А прямые АА1 и DС параллельны? Они пересекаются?

Значит, в пространстве есть прямые, которые не пересекаются, но не являются параллельными, т. к. не лежат в одной плоскости. Такие прямые называются скрещивающимися().

Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

У: Назовите скрещивающиеся прямые, которые встречаются у нас в классе. Рассмотрим алгоритм взаимного расположения двух прямых в пространстве.

Решение задач.

1. Всегда ли две непересекающиеся прямые в пространстве параллельы? (Устно).

2. Какие две прямые называются параллельными? (Устно).

3. Все грани – квадраты. Установите взаимное расположение прямых:

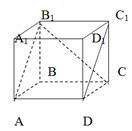
AD…A1D1; AB1… B1C1; AB1… DC1;

A1 D1 AD…B1C1; B1C1… DC1; BB1…DC.

Домашнее задание: Пункт 4, №16.

2. Урок: « Параллельность прямой и плоскости».

Объяснение нового материала.

У: Давайте ответим вместе на следующие вопросы:

· Назовите возможные варианты взаимного расположения прямой и плоскости. (Прямая принадлежит плоскости, прямая пересекает плоскость, прямая не лежит в плоскости).

· Сколько точек пересечения может иметь прямая и плоскость? (Одну, более одной, не иметь вообще). Обосновать ответ.

· Посмотрите вокруг. Назовите все варианты взаимного расположения прямой и плоскости в пространстве в нашем классе, и как называется такое расположение?

У: Теперь рассмотрим алгоритм взаимного расположения прямой и плоскости в пространстве:

· Рассмотрим прямую и плоскость.

· Рассмотрим расположение относительно точки

· Если пряма и плоскость в пространстве не имеют хотя бы одну общую точку, то они параллельны

· Если прямая и плоскость в пространстве имеют одну общую точку, то возможны два случая: либо более одной общей точки, либо только одна.

· Если точка только одна, то прямая и плоскость пересекаются

· Если более одной, то прямая принадлежит плоскости.

		а и α

Да Нет

Да Нет