Описание методики обучения учащихся темы «Параллельность прямых и плоскостей в курсе геометрии 7 – 11 классах»

У: Запишите этот алгоритм в тетрадь. Итак, так какие прямая и плоскость называются параллельными?

у: Пряма и плоскость называются параллельными, если они не имеют общих точек.

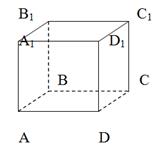
У: На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как установить параллельность прямой и плоскости? В силу бесконечности прямой и плоскости сделать это по определению очень трудно. Нужен признак параллельности прямой и плоскости.

Обратите внимание на модель куба. DC||(AA1B1). В плоскости (AA1B1) имеется прямая АВ, параллельная DC. DC||(A1B1С1). В плоскости (A1B1С1) имеется прямая D1C1, параллельная DC.

У: Попробуйте сформулировать признак параллельности прямой и плоскости.

Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой - нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Доказательство.

У: Рассмотрим плоскость α и две параллельные прямые а и b, расположенные так, что прямая b лежит в плоскости α, а прямая а не лежит в этой плоскости. Докажем, что а|| α. Предположим, что это не так. Тогда в какой плоскости будет лежать прямая а?

у: В плоскости α.

У: Верно. Но по лемме о пересечении плоскости параллельными прямыми прямая b тоже пересекает плоскость α. Но что сказано в условии про прямую b и плоскость α?

у: Что прямая b лежит в плоскости α? Поэтому это предположение невозможно.

У: Поэтому прямая а не пересекает эту плоскость, поэтому как расположены данная прямая к плоскости?

у: она параллельна данной плоскости.

У: теорема доказана.

3. Урок: «Скрещивающиеся прямые»

Опрос:

· Какие прямые называются параллельными?

· Какие прямые в плоскости называются пересекающиеся?

· Сколько общих точек при пересечении имеет плоскость и прямая? (два случая)

· Что значит: пряма и плоскость параллельны?

· Какие плоскости называются перпендикулярными?

· Какие плоскости называются параллельными?

Наглядно-поисковые задачи:

У: Даны рисунки на слайде. Укажите номера рисунков, являющимися ответом на следующие вопросы-задания.

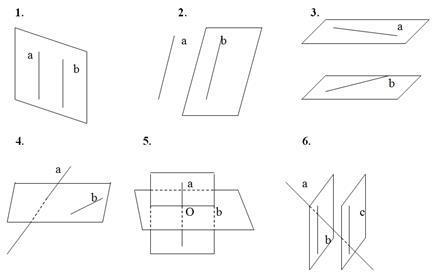
Вопросы (устно):

1. На каких рисунках изображены параллельные прямые? Обосновать ответ.

у: В 1, так как прямые лежат в одной плоскости и не имеют общих точек пересечения; во 2, так как прямые хоть и лежат в разных плоскостях, но не имеют общих точек, то есть не пересекаются; в 6 прямые b и c также не имеют точек пересечения.

2. Назовите перпендикулярные прямые? Ответ обосновать.

у: 5-й рисунок, так как угол (аОв) равен 900.

3. На каких рисунках изображены пересекающиеся прямые? Обосновать.

у: 5-й и 6-й рисунки, так как прямые имеют общую точку.

4. Назовите непересекающиеся прямые? Обосновать.

у: Непересекающиеся прямые не имеют общих точек, поэтому 1, 2, 3, 4 и 6 (b и c).

У: Вы прекрасно справились с заданиями. С их помощью мы вспомнили некоторые свойства прямых, которые понадобятся нам для усвоения сегодняшней темы «Скрещивающиеся прямые».

У: На какие группы можно разделить две прямые относительно плоскости?

у: Они могут лежать в одной плоскости, либо в разных плоскостях.

У: Рассмотрим прямые, которые лежат в одной плоскости. Разделим относительно общих точек две прямые.

у: Прямые либо имеют общую точку, либо не имеют.

У: Соответственно, какие названия они носят?

у: Пересекающиеся и параллельные.

У: Рассмотрим теперь прямые, которые не лежат в одной плоскости. Какие рисунки на слайде №3 можно отнести к этому описанию?