Описание методики обучения учащихся темы «Параллельность прямых и плоскостей в курсе геометрии 7 – 11 классах»

у: 2, 3, 4, 6 (прямые b и c).

У: Почему мы не отнесли к этой категории 5 рисунок?

у: Так как эти прямые лежат в одной плоскости.

У: Но если посмотреть внимательно на рисунки 2 и 6, то можно заметить, что можно провести плоскость через данные прямые, следовательно, они тоже могут лежать в одной плоскости. Чего не скажешь о рисунках 3 и 4.

У: Делаем вывод, что прямые на рисунке 3 и 4 - скрещивающиеся.

У: Рассмотрим решение следующей задачи. Доказать, что все прямые, пересекающие параллельные прямые, лежат в одной плоскости (стр.239)

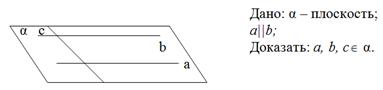
У: Решение

Так как данные прямые a и b параллельны, то через них можно провести плоскость. Смотрим на слайд. Обозначим эту плоскость . Сколько общих точек имеет прямая c с плоскостью , которая пересекает данные параллельные прямые?

у: Две.

У: Верно. Как называются такие точки?

у: Точи пересечения

У: Вспомним теорему, которую мы рассматривали ранее о том, что если две прямые лежат в одной плоскости и третья пересекает их, то эти три прямые лежат в одной плоскости. Какой вывод можно сделать относительно всех прямых, пересекающих a и b в плоскости ?

у: Они все лежат в плоскости .

У: Запишем решение на доске. Кто желает к доске?

Усвоение нового.

Работа с формулировкой теоремы

У: Рассмотрим параллельные прямые. Сколько точек достаточно для того, чтобы провести параллельную прямую относительно другой?

у: Одну.

У: Почему?

у: Так как остальные точки данной прямой будут лежать на том же расстоянии, что и данная.

У: Рассмотрим теорему, утверждающая этот факт и рассмотрим ее доказательство. Запишем в тетрадь: « Теорема. Через точку вне данной прямой можно провести прямую, параллельную данной, и при том только одну». (Слайд №6)

У: Замечание. Утверждение единственности в теореме не является простым следствием аксиомы параллельных, так как этой аксиомой утверждается единственность прямой, параллельной данной в данной плоскости. Поэтому она требует доказательства.

У: Проведем доказательство (слайд №7)

Пусть а - данная прямая и точка А – точка, не лежащая на этой прямой. Проведем через точку А и прямую а плоскость . Почему такую плоскость можно провести?

у: Плоскость можно провести через три любые точки. А так как нам дана точка А и две любые точки на прямой а, поэтому такая плоскость существует.

У: Верно. Теперь проведем а1, лежащую в и параллельную прямой а. Докажем, что а1, параллельная а, единственная. Допустим, что существует другая прямая, проходящая через точку А и параллельная прямой а. Проведем плоскость . Через какие точки она проходит?

у: Через точку А и две точки, лежащие на прямой а, то есть через точку А и прямую а.

У: Что мы можем сказать о плоскостях и ?

у: совпадает с , так как проходят через точку А и прямую а.

У: Верно. Теперь по аксиоме параллельных прямые а1 и а2 совпадают. Теорема доказана.

4. Урок: «Параллельность плоскостей»

Объяснение нового материала.

У: Посмотрите на стены и пол в нашем классе. Каково взаимное расположение стены и потолка?

у: Они пересекаются по прямой.

У: Каково взаимное расположение пола и потолка?

у: Они не пересекаются, т. е. параллельны.

У: Делаем вывод: если две плоскости имеют общую точку, то они пересекаются по прямой – это нам известно. Отсюда следует, что две плоскости либо пересекаются по прямой, либо на пересекаются, т. е. не имеют ни одной общей точки. Исходя из этих фактов, какие прямые мы будем называть параллельными?